Wibble: Day 4

I had a few options for what to work on today, but decided to tackle two tasks:

1. When a tile is used in a chain, it is replaced with a random letter.

2. When selecting a random letter, base it on the letter’s frequency in the English language rather than pure randomness.

Replacing Used Letters

This was a simple feature to implement. Since the game already knows which tiles were used via the currentChain array, all I have to do is iterate through the chain and use the stored indices of each tile to replace them with a new random tile. This requires some house cleaning, however. The process of replacing tiles is a cleanup step that seems independent of either the “score” state or the “idle” state. Instead of adding an entirely new state, I renamed the “score” state as the “clean up” state and made it responsible for handling post-chaining processes, such as updating the total score and replacing used letters.

Intelligently Selecting Random Letters

By “intelligently,” I mean selecting the letters such that you would see an uneven random distribution, where some letters are more likely than others. This is different than the current method, where I use JavaScript’s Math.random() to select tiles. Math.random() is configured to produce a uniform distribution where all possible output values are equally likely. This is undesirable for a game about making a word as long as possible since you could end up with a board full of letters that are unlikely to make up an English word.

To fix this, I referenced the frequency of letters in the English alphabet. For the purposes of Wibble, I specifically chose the frequencies of each letter in normal prose rather than in the dictionary since the former matched up closer to the scores of the tiles. (Scrabble uses the frequency of letters to inform how many points a letter is worth, so the less frequently a letter is used, the higher the score.)

While knowing these frequencies is nice, they don’t exactly lend themselves to selecting each letter in a way I am familiar with. A quick search on the Internet for “randomly selecting values based on weight” led me to a StackOverflow post that pointed me towards using a “discrete cumulative density function.”

According to Wikipedia, “cumulative density function” is a misnomer that confuses two different but related statistical concepts: probability density functions and cumulative distribution functions.

Probability Density Functions and Cumulative Distribution Functions

Wikipedia wasn’t much help in understanding either probability density functions (PDFs) or cumulative distribution functions (CDFs), so I turned to an alternative source and will try to abbreviate what I learned here:

A discrete probability density function is a function that takes an outcome as an input and outputs the probability of that outcome. For instance, for a fair six-sided die, we would have a probability function that looks like this:

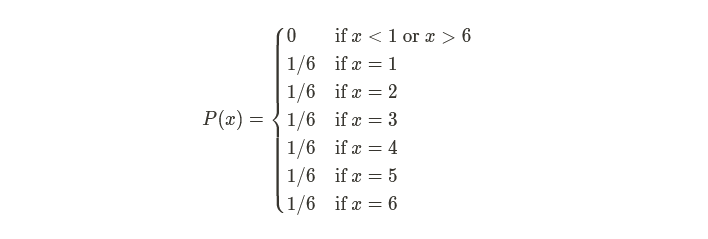
A discrete cumulative density function is a function that, like a PDF, takes an outcome as an input. Still, instead of outputting the probability of that outcome, it outputs the sum of the probability of that outcome and all outcomes of equal or lesser probability. As an example, if I were to create a CDF of the fair six-sided die, it would look like this:

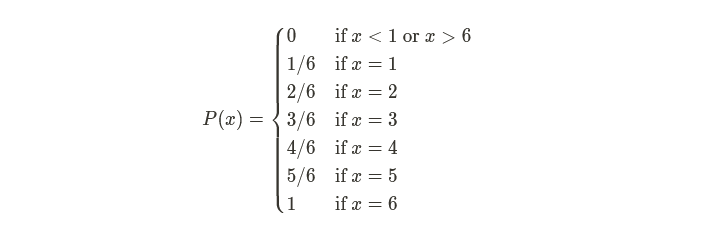
A CDF can be used to randomly select any $x$ by generating a random value between 0 and 1, then checking if that value is less than or equal to $P(x)$ but greater than $P(x-1)$.

Using Spreadsheets to Build the Cumulative Density Function for Wibble

The table on Wikipedia gave me the PDF of the alphabet — the probability density function describing how probable a letter in the English alphabet is. Now I needed to generate a CDF to select the letters using the regular Math.random() call. Since the PDF will never be updated during runtime, the CDF will always be the same on every execution, so I can save myself some time and just compute the CDF in Google Sheets and paste the result into Wibble:

const tileCDF = {
  Z: [0, 0.00074],
  Q: [0.00074, 0.00169],
  J: [0.00169, 0.00319],
  X: [0.00319, 0.00469],
  K: [0.00469, 0.01239],
  V: [0.01239, 0.02219],
  B: [0.02219, 0.03719],
  P: [0.03719, 0.05619],
  G: [0.05619, 0.07619],
  Y: [0.07619, 0.09619],
  F: [0.09619, 0.11819],
  M: [0.11819, 0.14219],
  W: [0.14219, 0.16619],
  C: [0.16619, 0.19419],
  U: [0.19419, 0.22219],
  L: [0.22219, 0.26219],
  D: [0.26219, 0.30519],
  R: [0.30519, 0.36519],
  H: [0.36519, 0.42619],
  S: [0.42619, 0.48919],
  N: [0.48919, 0.55619],
  I: [0.55619, 0.62619],
  O: [0.62619, 0.70119],
  A: [0.70119, 0.78319],
  T: [0.78319, 0.87419],
  E: [0.87419, 1]
}

Notice that this table is sorted by frequency, with the least frequent letters at the top and the most frequent at the bottom. This is important because of the next step: searching the table for the range that fits our random value.

Searching Through the Cumulative Density Function Table For Our Random Letter

The Stackoverflow answer that led me to use a CDF in the first place recommended using binary search to search through the array optimally. Binary search requires sorting the array, which we conveniently did in Google Sheets.

With the input sorted, the binary sort algorithm works like this:

1. Find the index in the middle of your array.

2. Compare the value in the middle of the array to your target value.

3. If your target value is less than the value in the middle of the array, perform a binary search on all array values below the middle of the array.

4. If your target value is greater than the value in the middle of the array, perform a binary search on all values above the middle of the array.

5. If your target value matches the value in the middle of the array, return that you have found the item you are looking for.

6. If there are no more values in the array to search, return that you didn’t find the array.

And in code, it would look like this:

function binarySearch (array, target) {
	const index = Math.trunc(array.length / 2)
	
	if (array.length === 1) {
		return array[index] === target;
	}
	else if (target === array[index]) {
		return true;
	}
	else if (target < array[index]) {
		return binarySearch(array.slice(0, index), target);
	}
	else if (array[index] < target) {
		return binarySearch(array.slice(index));
	}
}

This needs to be heavily modified to work with our CDF, however. First, we are not looking for a specific value but rather checking that our target fits a specific range. This means that all comparisons have to be rewritten to check the target against the upper and lower bounds:

function binarySearch (cdfIntervals, target) {
	const index = Math.trunc(array.length / 2);
	const [lowerBound, upperBound] = cdfIntervals[index];
	
	if (array.length === 1) {
		return (lowerBound < target) && (target <= upperBound);
	}
	else if ((lowerBound < target) && (target <= upperBound)) {
		return true;
	}
	else if (target <= lowerBound) {
		return binarySearch(array.slice(0, index), target);
	}
	else if (upperBound < target) {
		return binarySearch(array.slice(index));
	}
}

The next modification is that we don’t just want to know that the target value fits in an interval stored in our CDF. We actually want to know which interval in our CDF the target fits inside of:

function binarySearch (cdfIntervals, target, indexOffset = 0) {
	const index = Math.trunc(array.length / 2);
	const [lowerBound, upperBound] = cdfIntervals[index];
	
	if (array.length === 1) {
		return (lowerBound < target) && (target <= upperBound)
			? index + indexOffset
			: -1;
	}
	else if ((lowerBound < target) && (target <= upperBound)) {
		return index + indexOffset;
	}
	else if (target <= lowerBound) {
		return binarySearch(array.slice(0, index), target, indexOffset);
	}
	else if (upperBound < target) {
		return binarySearch(array.slice(index), target, indexOffset + index);
	}
}

Not only do I return the index (or -1 if no index was found), but I also pass along a parameter called indexOffset. This is an artifact of using the slice function when we pass the array to the nested call. Because the slice is an entirely new array with no knowledge of the array it was made from, the index returned by that nested call will only be relative to that slice, not the original input array. In the best case, this doesn’t matter, but in the worst case, we will receive an index of 0 when we wanted an index of 12. To fix this, I pass some context down to the nested function in the form of an indexOffset. This is essentially the true position of the slice’s index 0 relative to the original input array. Adding the indexOffset to the index before returning, it ensures that whatever is returned will be relative to the original input array and not a slice of that array.

But getting the correct index is only part of what I need. My binary search assumes that all indices are numeric, but my CDF uses the letters as indices. This means that I have to use Object.values to extract the array of values from the CDF, get the numeric index during the binary search, then use the numeric index to get the letter using Object.keys:

const i = binarySearch(Object.values(tileCDF), Math.random())
const letter = Object.keys(tileCDF)[i]

Then with the letter, I can grab the appropriate tile data:

tiles.find(({ letter }) => letter === l)

This version of Wibble is hosted at: https://wibble-day-4.vercel.app. The code can also be found on my GitHub.